Ratios make baking a piece of cake
You’ve got your eggs, your butter, your flour, your sugar and chocolate. You’ve got your gran’s best recipe for chocolate cake. You’re all ready and all set to cook - and then trouble strikes. The recipe’s all in ounces and pints and you can’t find a set of scales anyway. What do you do? Add the secret ingredient, ratio..
Flour, eggs, sugar and butter are the main ingredients in baked treats - that includes biscuits, bread, pastry and cakes. The magic which changes these raw ingredients into a baker’s product comes from ratios (and a bit of heating).
 Flour and eggs both contain proteins, long molecules which get tangled up in each other. These give structure and hold things together.
Flour and eggs both contain proteins, long molecules which get tangled up in each other. These give structure and hold things together.
Moistness comes from the fat in the cake - which could be butter or oil - and the sugars. These sticky substances do the opposite and soften the food, making it crumbly.
So if you have too much butter and sugar, your (for example) cake may fall apart or stay runny. On the other hand if you put too much flour and egg in, the cake will be dry and tough. When making up a recipe bakers know which proportions they must mix their ingredients to get a good basic texture. Then fine tuning comes in to make the difference between a delicate crumbly walnut cake and a sticky carrot cake.
Weighing it up
So what are these balances you should be aiming for? Well, after millennia of baking, this is what has been found to work:
Cakes are made by combining 1 part sugar with 1 part butter or other fat, 1 part flour, and 1 part eggs. After a good beating to get lots of air inside the mixture, this makes a batter which will rise to be soft and moist.Biscuits, on the other hand, just require 1 part sugar, one part fat, and one part flour.While to make pancakes, you need 2 parts liquid (usually milk), 2 parts egg and 1 part flour.

Remember; measurements are by weight, not volume!
You can also convert a regular recipe - maybe a family speciality - into a ratio form using the techniques you learn in maths. But why would you want to do that?
Rationing is good for you
Cooking using ratios is much easier than working from a set recipe. It means that:
you can work without scales if you haven’t got anyyou can scale up and scale down recipes really easily. No need to recalculate everything if you’ve only got one egg - or only one friend coming round.ingredients can be substituted in and out easily - sunflower spread instead of butter for vegans, or rice flour instead of flour for coeliacsthe numbers are nice whole numbers, easy to remember
Bringing your maths into the kitchen can give you tasty results and liberate you from slavishly following recipes.






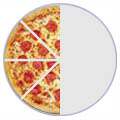
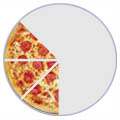 1/21/43/8
1/21/43/8
 =
= =
=