 Medicine :
Medicine :
HourStartEnd12009/10 x 200 = 18021809/10 x 180 = 16231629/10 x 162 = 145.8...
The sequence of numbers shown above is geometric because there is a common ratio between terms, in this case 9/10. Doctors can use this idea to quickly decide how often a patient needs to take their prescribed medication.
Ratios and Proportions
Nurses also use ratios and proportions when administering medication. Nurses need to know how much medicine a patient needs depending on their weight. Nurses need to be able to understand the doctor’s orders. Such an order may be given as: 25 mcg/kg/min. If the patient weighs 52kg, how many milligrams should the patient receive in one hour? In order to do this, nurses must convert micrograms (mcg) to milligrams (mg). If 1mcg = 0.001mg, we can find the amount (in mg) of 25mcg by setting up a proportion.

By cross-multiplying and dividing, we see that 25mcg = 0.025mg. If the patient weighs 52kg, then the patient receives 0.025(52) = 1.3mg per minute. There are 60 minutes in an hour, so in one hour the patient should receive 1.3(60) = 78mg. Nurses use ratios and proportions daily, as well as converting important units. They have special “shortcuts” they use to do this math accurately and efficiently in a short amount of time.
Numbers give doctors much information about a patient’s condition. White blood cell counts are generally given as a numerical value between 4 and 10. However, a count of 7.2 actually means that there are 7200 white blood cells in each drop of blood (about a microlitre). In much the same way, the measure of creatinine (a measure of kidney function) in a blood sample is given asX mg per deciliter of blood. Doctors need to know that a measure of 1.3 could mean some extent of kidney failure. Numbers help doctors understand a patient’s condition. They provide measurements of health, which can be warning signs of infection, illness, or disease.
Body Mass Index
In terms of medicine and health, a person’s Body Mass Index (BMI) is a useful measure. Your BMI is equal to your weight in pounds, times 704.7, divided by the square of your height in inches. This method is not always accurate for people with very high muscle mass because the weight of muscle is greater than the weight of fat. In this case, the calculated BMI measurement may be misleading. There are special machines that find a person’s BMI. We can find the BMI of a 145-pound woman who is 5’6” tall as follows.
First, we need to convert the height measurement of 5’6” into inches, which is 66”. Then, the woman’s BMI would be:

This is a normal Body Mass Index. A normal BMI is less than 25. A BMI between 25 and 29.9 is considered to be overweight and a BMI greater than 30 is considered to be obese. BMI measurements give doctors information about a patient’s health. Doctor’s can use this information to suggest health advice for patients. The image below is a BMI table that gives an approximation of health and unhealthy body mass indexes.

Image reproduced with permission of Health Canada
CAT Scans
One of the more advanced ways that medical professionals use mathematics is in the use of CAT scans. A CAT scan is a special type of x-ray called a Computerized Axial Tomography Scan. A regular x-ray can only provide a two-dimensional view of a particular part of the body. Then, if a smaller bone is hidden between the x-ray machine and a larger bone, the smaller bone cannot be seen. It is like a shadow.

Image reproduced with permission of NeuroCognition Laboratory
It is much more beneficial to see a three dimensional representation of the body’s organs, particularly the brain. CAT scans allow doctors to see inside the brain, or another body organ, with a three dimensional image. In a CAT scan, the x-ray machine moves around the body scanning the brain (or whichever body part is being scanned) from hundreds of different angles. Then, a computer takes all the scans together and creates a three dimensional image. Each time the x-ray machine makes a full revolution around the brain, the machine is producing an image of a thin slice of the brain, starting at the top of the head and moving down toward the neck. The three-dimensional view created by the CAT scan provides much more information to doctors that a simple two-dimensional x-ray.
Mathematics plays a crucial role in medicine and because people’s lives are involved, it is very important for nurses and doctors to be very accurate in their mathematical calculations. Numbers provide information for doctors, nurses, and even patients. Numbers are a way of communicating information, which is very important in the medical field.
Another application of mathematics to medicine involves a lithotripter. This is a medical device that uses a property of an ellipse to treat gallstones and kidney stones. To learn more, visit the Lithotripsy page.






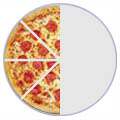
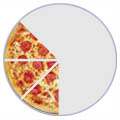 1/21/43/8
1/21/43/8
 =
= =
=













